Difference between revisions of "Damped oscillation"
Max Peschke (talk | contribs) m |
Max Peschke (talk | contribs) |
||
| Line 1: | Line 1: | ||
| + | [[File:ExecutionOfAnAnalogSimulation.jpg|thumb]] | ||
The modeling of a '''damped oscillation''' is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on '''The Analog Thing''' using the full repatriation method to derive a computer circuit and to get results on an oscilloscope. | The modeling of a '''damped oscillation''' is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on '''The Analog Thing''' using the full repatriation method to derive a computer circuit and to get results on an oscilloscope. | ||
| − | == Mathematical description of a damped oscillation == | + | There are four major steps, which are equally crucial: |
| + | # Describe the to be simulated system with differential equations | ||
| + | # Derive a computer circuit from these equations | ||
| + | # Wire the computer circuit on the analog computer and adjust parameters | ||
| + | # Choose viable visualization method (usually oscilloscopes) and connect the computer circuit | ||
| + | |||
| + | == 1. Mathematical description of a damped oscillation == | ||
[[File:Damped oscillator.png|thumb]] | [[File:Damped oscillator.png|thumb]] | ||
The first and often the hardest step of modeling any to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations. | The first and often the hardest step of modeling any to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations. | ||
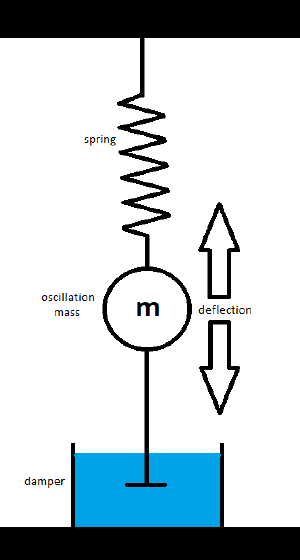
Find all acting forces, three in this case: | Find all acting forces, three in this case: | ||
| − | - Spring force F<sub>s</sub> = k*x; | + | - '''Spring force F<sub>s</sub> = k*x;''' |
| − | - Inertia force F<sub>m</sub> = m*a; | + | k = spring coefficient, x = deflection |
| − | - Damper force F<sub>d</sub> = d*v; | + | - '''Inertia force F<sub>m</sub> = m*a;''' |
| + | m = mass, a = acceleration | ||
| + | - '''Damper force F<sub>d</sub> = d*v;''' | ||
| + | d = damper coefficient, v = velocity | ||
Set the sum of all forces to zero (definition of an isolated system): | Set the sum of all forces to zero (definition of an isolated system): | ||
F<sub>m</sub> + F<sub>d</sub> + F<sub>s</sub> = 0 | F<sub>m</sub> + F<sub>d</sub> + F<sub>s</sub> = 0 | ||
m*a + d*v + k*x = 0 | m*a + d*v + k*x = 0 | ||
Replace the velocity '''v''' with '''ẋ''' and the acceleration '''a''' with '''ẍ''' | Replace the velocity '''v''' with '''ẋ''' and the acceleration '''a''' with '''ẍ''' | ||
| − | v = ẋ (the velocity equals the first derivative of x) | + | '''v = ẋ''' |
| − | a = ẍ (the acceleration equals the second derivative of x) | + | (the velocity equals the first derivative of x) |
| + | '''a = ẍ''' | ||
| + | (the acceleration equals the second derivative of x) | ||
m*a + d*v + k*x | m*a + d*v + k*x | ||
= m*ẍ + d*ẋ + k*x = 0 | = m*ẍ + d*ẋ + k*x = 0 | ||
| Line 20: | Line 32: | ||
Lastly, solve this equation for the highest derivative the finish the full repatriation: | Lastly, solve this equation for the highest derivative the finish the full repatriation: | ||
| − | -> ẍ = -(d*ẋ + k*x) / m | + | -> '''ẍ = -(d*ẋ + k*x) / m''' |
| + | |||
| + | == 2. Derivation of a computer circuit == | ||
Revision as of 13:36, 6 December 2021
The modeling of a damped oscillation is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on The Analog Thing using the full repatriation method to derive a computer circuit and to get results on an oscilloscope.
There are four major steps, which are equally crucial:
- Describe the to be simulated system with differential equations
- Derive a computer circuit from these equations
- Wire the computer circuit on the analog computer and adjust parameters
- Choose viable visualization method (usually oscilloscopes) and connect the computer circuit
1. Mathematical description of a damped oscillation
The first and often the hardest step of modeling any to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations.
Find all acting forces, three in this case:
- Spring force Fs = k*x;
k = spring coefficient, x = deflection
- Inertia force Fm = m*a;
m = mass, a = acceleration
- Damper force Fd = d*v;
d = damper coefficient, v = velocity
Set the sum of all forces to zero (definition of an isolated system):
Fm + Fd + Fs = 0 m*a + d*v + k*x = 0
Replace the velocity v with ẋ and the acceleration a with ẍ
v = ẋ
(the velocity equals the first derivative of x)
a = ẍ
(the acceleration equals the second derivative of x)
m*a + d*v + k*x
= m*ẍ + d*ẋ + k*x = 0
Now we have an exact description the damped oscillation in the form of a differential equation.
Lastly, solve this equation for the highest derivative the finish the full repatriation:
-> ẍ = -(d*ẋ + k*x) / m