Damped oscillation

The modeling of a damped oscillation is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on The Analog Thing using the full repatriation method to derive a computer circuit (originally developed by Lord Kelvin around 1875) and to get results on an oscilloscope.

There are four major steps, all of which are equally crucial:

1. Describe the to be simulated system with differential equations
2. Derive a computer circuit from these equations
3. Wire the computer circuit on the analog computer and adjust parameters
4. Choose viable visualization method (usually oscilloscopes) and connect the computer circuit

This article will focus on point 2. to 4. and requires a basic understanding of differential equations.

1. Mathematical description of a damped oscillation

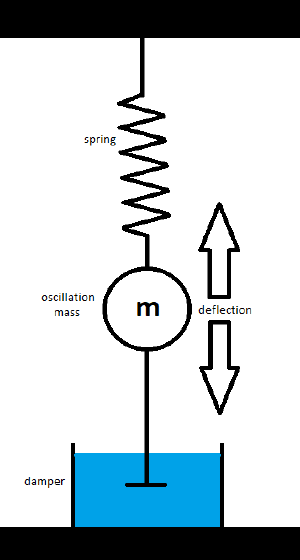
The first and often hardest step of modeling a to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations. For this example the description is rather short:

Find all acting forces, three in this case:

  - Spring  force Fs = k*x;
    k = spring coefficient, x = deflection
  - Inertia force Fm = m*a;
    m = mass, a = acceleration
  - Damper  force Fd = d*v;
    d = damper coefficient, v = velocity

Set the sum of all forces to zero (definition of an isolated system):

  Fm  + Fd  + Fs  = 0
  m*a + d*v + k*x = 0

Replace the velocity v with ẋ and the acceleration a with ẍ

  v = ẋ
(the velocity equals the first derivative of x)
  a = ẍ
(the acceleration equals the second derivative of x)
    m*a + d*v + k*x 
  = m*ẍ + d*ẋ + k*x = 0

Now we have an exact description the damped oscillation in the form of a differential equation.

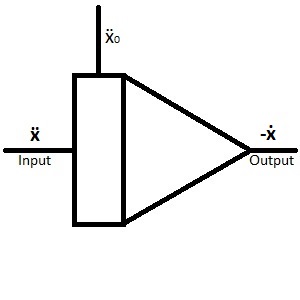
Lastly, solve this equation for the highest derivative the finish the full repatriation:

-> ẍ = -(d*ẋ + k*x) / m

2. Derivation of a computer circuit

Basic Integrator Scheme