Difference between revisions of "Damped oscillation"
Max Peschke (talk | contribs) |
Max Peschke (talk | contribs) m |
||
| Line 1: | Line 1: | ||
[[File:ExecutionOfAnAnalogSimulation.jpg|thumb]] | [[File:ExecutionOfAnAnalogSimulation.jpg|thumb]] | ||
| − | The modeling of a '''damped oscillation''' is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on '''The Analog Thing''' using the full repatriation method to derive a computer circuit and to get results on an oscilloscope. | + | The modeling of a '''damped oscillation''' is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on '''The Analog Thing''' using the full repatriation method to derive a computer circuit (originally developed by Lord Kelvin around 1875) and to get results on an oscilloscope. |
| − | There are four major steps, which are equally crucial: | + | There are four major steps, all of which are equally crucial: |
# Describe the to be simulated system with differential equations | # Describe the to be simulated system with differential equations | ||
# Derive a computer circuit from these equations | # Derive a computer circuit from these equations | ||
# Wire the computer circuit on the analog computer and adjust parameters | # Wire the computer circuit on the analog computer and adjust parameters | ||
# Choose viable visualization method (usually oscilloscopes) and connect the computer circuit | # Choose viable visualization method (usually oscilloscopes) and connect the computer circuit | ||
| + | |||
| + | This article will focus on point 2. to 4. and requires a basic understanding of differential equations. | ||
== 1. Mathematical description of a damped oscillation == | == 1. Mathematical description of a damped oscillation == | ||
[[File:Damped oscillator.png|thumb]] | [[File:Damped oscillator.png|thumb]] | ||
| − | The first and often | + | The first and often hardest step of modeling a to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations. |
| + | For this example the description is rather short: | ||
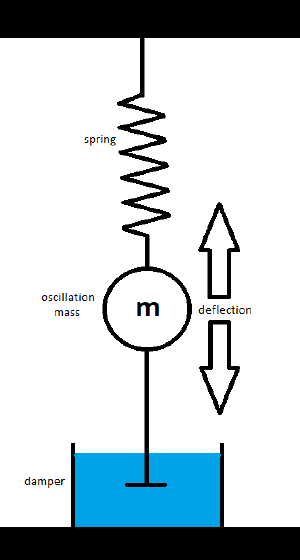
Find all acting forces, three in this case: | Find all acting forces, three in this case: | ||
Revision as of 13:51, 6 December 2021
The modeling of a damped oscillation is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on The Analog Thing using the full repatriation method to derive a computer circuit (originally developed by Lord Kelvin around 1875) and to get results on an oscilloscope.
There are four major steps, all of which are equally crucial:
- Describe the to be simulated system with differential equations
- Derive a computer circuit from these equations
- Wire the computer circuit on the analog computer and adjust parameters
- Choose viable visualization method (usually oscilloscopes) and connect the computer circuit
This article will focus on point 2. to 4. and requires a basic understanding of differential equations.
1. Mathematical description of a damped oscillation
The first and often hardest step of modeling a to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations. For this example the description is rather short:
Find all acting forces, three in this case:
- Spring force Fs = k*x;
k = spring coefficient, x = deflection
- Inertia force Fm = m*a;
m = mass, a = acceleration
- Damper force Fd = d*v;
d = damper coefficient, v = velocity
Set the sum of all forces to zero (definition of an isolated system):
Fm + Fd + Fs = 0 m*a + d*v + k*x = 0
Replace the velocity v with ẋ and the acceleration a with ẍ
v = ẋ
(the velocity equals the first derivative of x)
a = ẍ
(the acceleration equals the second derivative of x)
m*a + d*v + k*x
= m*ẍ + d*ẋ + k*x = 0
Now we have an exact description the damped oscillation in the form of a differential equation.
Lastly, solve this equation for the highest derivative the finish the full repatriation:
-> ẍ = -(d*ẋ + k*x) / m