Rotation matrix

This page describes Electronics to implement 3-dimensional coordinate transformations in terms of a rotation matrix. The most typical use case is some analog circuit which computes the 3-dimensional particle trajectory (x,y,z). This three-dimensional space is typically projected on the two dimensional oscilloscope screen by just showing some plane, for instance the z-plane, so that (x,y) are visible. By means of a physical rotation matrix, you can rotate the (x,y,z) space so that you can see a two-dimensional image (projection) from an arbitrary direction.

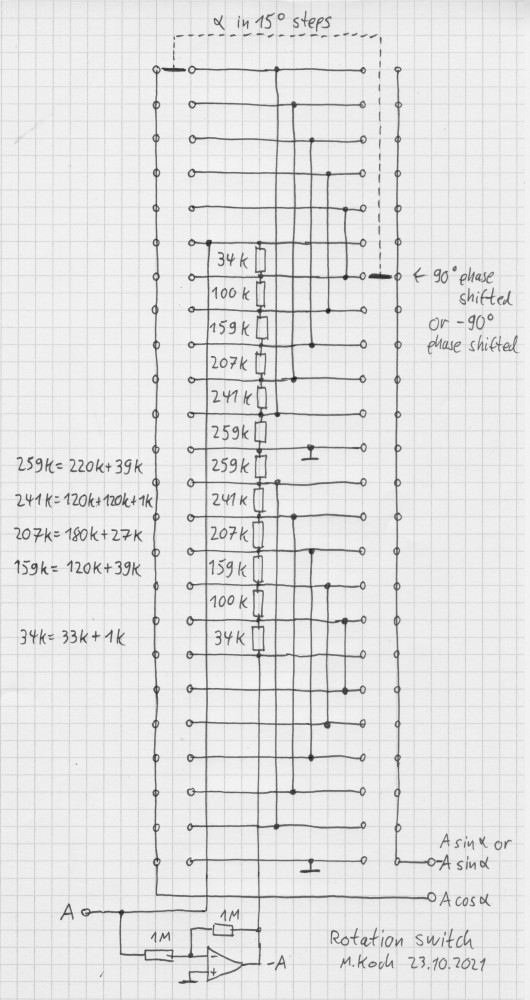
A 24-step switch can be used for angle adjustment in 15° steps. These 4x24 switches are available on Aliexpress for less than 10€. Search for "4*24 Rotary Switch".

The switch must be disassembled to remove the limiter, so that the axis can be rotated over the full 360° range.

In those planes that make the sin() and -sin() signals, the contact must be removed from the A position and inserted in position B, which is 90° phase shifted from A. For the -sin() signal, the phase shift is in the other direction.

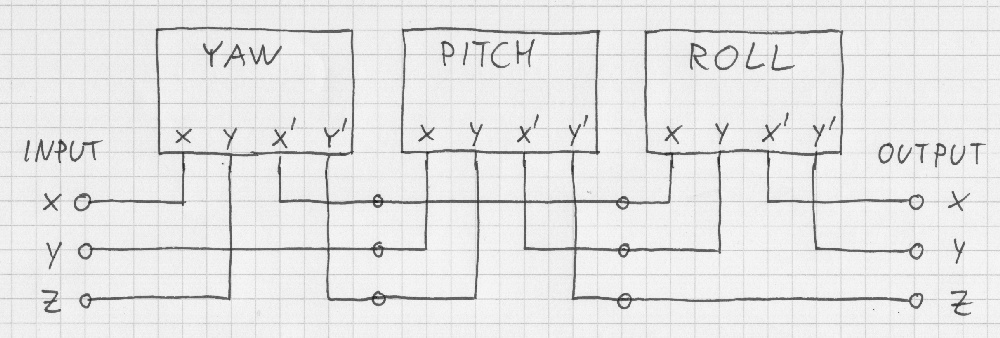
For yaw, pitch and roll rotations you need three switches.

This is the schematic for half of the switch. It has an input A and two outputs A*sin(alpha) and A*cos(alpha). The schematic for the other half is identical, but the contact in the switch is phase shifted in the other direction so that the outputs are -A*sin(alpha) and A*cos(alpha).

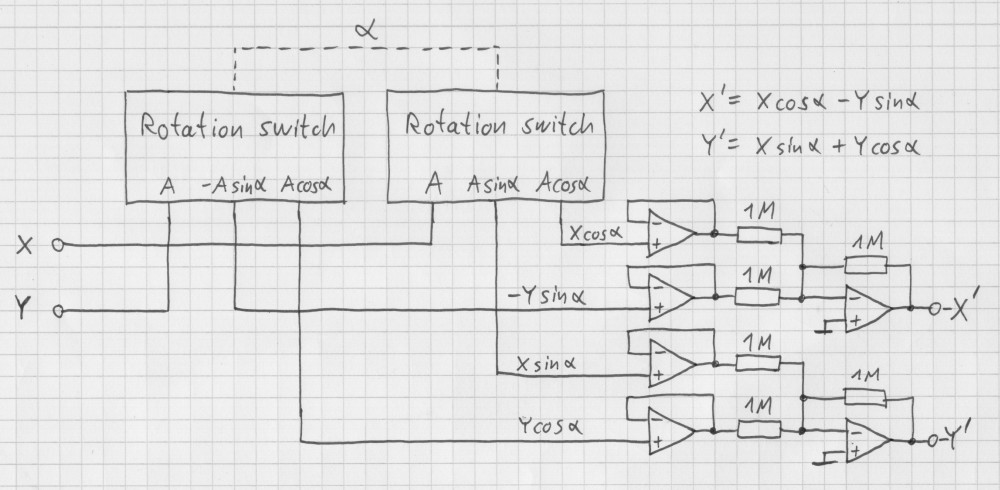
This is the main schematic:

It doesn't matter that the outputs X' and Y' are inverted. Just rotate the switch 180° to invert the signs.

Three rotators can be combined for making yaw, pitch and roll rotations: