Damped oscillation

Execution of an analog simulation

The modeling of a damped oscillation is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on The Analog Thing using the full repatriation method to derive a computer circuit (originally developed by Lord Kelvin around 1875) and to get results on an oscilloscope.

There are four major steps to execute a simulation on an analog computer, all of which are equally crucial:

1. Describe the to be simulated system with differential equations
2. Derive a computer circuit from these equations
3. Wire the computer circuit on the analog computer and adjust parameters
4. Choose viable visualization method (usually oscilloscopes) and connect the computer circuit

This article will focus on point 2. to 4. and requires a basic understanding of differential equations.

1. Mathematical description of a damped oscillation

Basic model of a damped oscillation

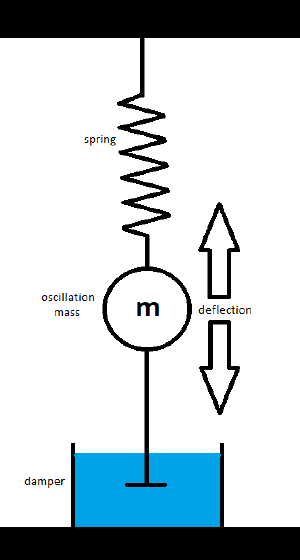
The first and often hardest step of modeling a to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations. For this example the description is rather short:

Find all acting forces, three in this case:

  - Spring  force Fs = k*x;
    k = spring coefficient, x = deflection
  - Inertia force Fm = m*a;
    m = mass, a = acceleration
  - Damper  force Fd = d*v;
    d = damper coefficient, v = velocity

Set the sum of all forces to zero (definition of an isolated system):

  Fm  + Fd  + Fs  = 0
  m*a + d*v + k*x = 0

Replace the velocity v with ẋ and the acceleration a with ẍ

  v = ẋ
(the velocity equals the first derivative of x)
  a = ẍ
(the acceleration equals the second derivative of x)
    m*a + d*v + k*x 
  = m*ẍ + d*ẋ + k*x = 0

Now we have an exact description the damped oscillation in the form of a differential equation.

Lastly, solve this equation for the highest derivative the finish the full repatriation:

-> ẍ = -(d*ẋ + k*x) / m

2. Derivation of a computer circuit

At first, we need three basic computing elements which can probably be found on every electrical analog computer:

Description	Circuit
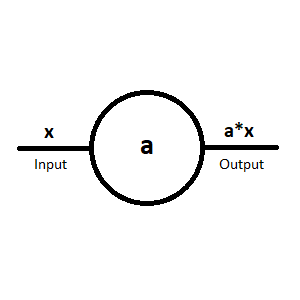
The coefficient potentiometer, which is used to multiply an input x with the factor a so a*x is generated. Note: a can only accept values between 0 and 1! Can also be used as dividing factor so a/x is generated. (That's unclear and should be explained)	Coefficient potentiometer Scheme
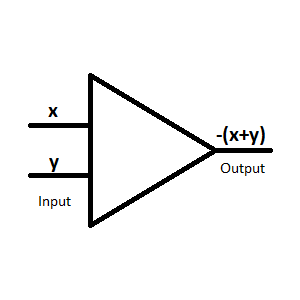
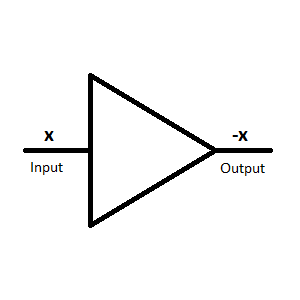
The inverter // summer, the input (or inputs) can be found on the left and the output on the right. Note: Due to technical reasons the output of a summer is negated! Input: x,y --> Output: -(x+y) At the basis of the output inversion a summer with one input functions as inverter and therefore the summer and the inverter share the same circuit symbol.	Basic Summer Scheme Basic Inverter Scheme
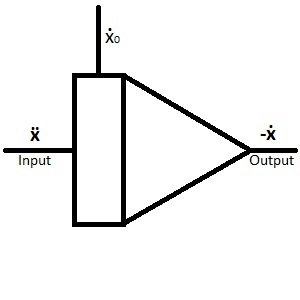
The integrator, the input (or inputs) can be found on the left and the output on the right. Coming from above you find ẋ0, which represents the starting condition of the integrator (often referred to initial condition) and can be thought of as the integration constant. When there is no initial condition drawn in the circuit, it is set to 0. Note: Due to technical reasons the output of an integrator is negated! ẍ -->-ẋ Electrical analog integrators can only integrate over time.	Basic Integrator Scheme

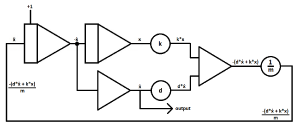
With these basic computing elements we are able to generate ẍ = -(d*ẋ + k*x) / m.

The basic idea is to start with an integrator assuming ẍ as it´s input. From there on you add computing elements do generate the input in the form of -(d*ẋ + k*x) / m.

Description	Circuit
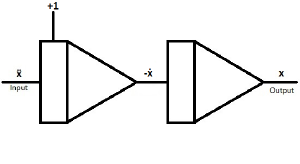
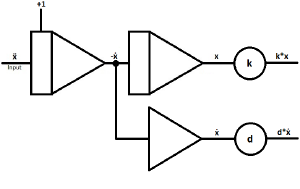
As mentioned above, start with an integrator and assume the highest derivative as input. ẍ represents the deflection over time. If ẍ0 is set to 1, the damped oscillation starts with maximum velocity. Possible error, don't you mean "If ẋ0 is set to 1, ..." ?	Basic integrator
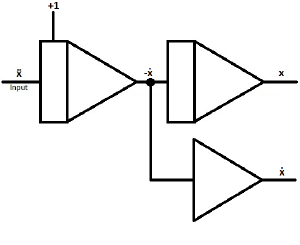
When putting another integrator behind the first, you can generate -ẋ and x	Generating all derivatives
To generate ẋ from -ẋ, branch off the circuit behind the first integrator and put the second wire in an inverter.	Generating all derivatives with correct sign
Insert two coefficient potentiometers to give ẋ and x their coefficients. k = spring coefficient d = damper coefficient To generate d*ẋ and k*x	Using of coefficient potentiometers to multiply parameters with a constant value
Merge the outputs of the coefficient potentiometers in a summer. Note the sign change, which is rather useful for this case. Output: -(d*ẋ + k*x)	Merging the potentiometer outputs in a summer
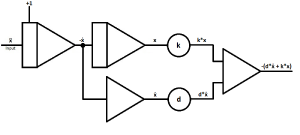
As last computing part add another coefficient potentiometer to divide the output of the summer with the mass coefficient. Output: -(d*ẋ + k*x) / m	Adding a potentiometer to add mass coefficient
Next to final step is to close the computing circuit by connecting the output of the last potentiometer with the input of the first integrator. The sign is already correct.	Closing the circuit
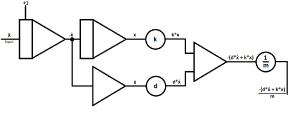
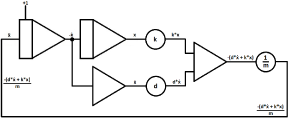
Lastly, branch of the circuit at a given point to use it later on with a given interface. In this case the circuit is branched just after the inverter to make the signal (in this case the velocity over time) visible on an oscilloscope later on. Usually, outputs are drawn as arrows.	Final circuit

3. Wiring the circuit on a THAT and adjusting parameters

Description	Circuit/Images
Example	Example
Example	Example
Example	Example
Example	Example
Example	Example