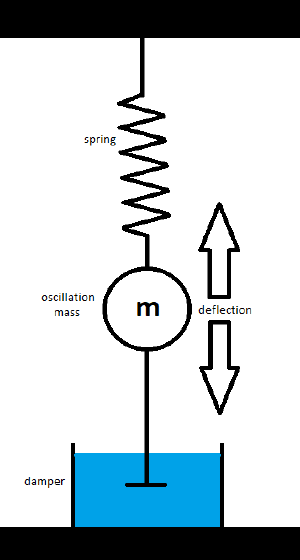
Damped oscillation

The modeling of a damped oscillation is a good starting point for analog programming beginners. This article shall give a detailed explanation how to implement a simulation on The Analog Thing using the full repatriation method and to get results on an oscilloscope.

Mathematical description of a damped oscillation

The first and often the hardest step of modeling any to be simulated system on an analog computer is to give an exact mathematical description of the system in the form of differential equations.

Find all acting forces, three in this case:

  - Spring  force Fs = k*x;     k = spring coefficient, x = deflection
  - Inertia force Fm = m*a;     m = mass, a = acceleration
  - Damper  force Fd = d*v;     d = damper coefficient, v = velocity

Set the sum of all forces to zero (definition of an isolated system):

  Fm  + Fd  + Fs  = 0
  m*a + d*v + k*x = 0

Replace the velocity v with ẋ and the acceleration a with ẍ

  v = ẋ (the velocity equals the first derivative of x)
  a = ẍ (the acceleration equals the second derivative of x)
    m*a + d*v + k*x 
  = m*ẍ + D*ẋ + k*x = 0

Now we have an exact description the damped oscillation in the form of a differential equation.

Lastly, solve this equation for the highest derivative the finish the full repatriation:

-> ẍ = -(d*ẋ + k*x) / m