Contents

• Elegant Chaos

  • Introduction

  • A jerk system

  • Nosé-Hoover Oscillator

  • References

Elegant Chaos

Introduction

One of the most intriguing books on chaotic systems is which is a true treasure trove for everybody fascinated by these mathematical objects. In the following, we will implement two of these systems on an analog computer.

A jerk system

So-called jerk systems are special cases of autonomous dissipative systems.The system under consideration in the following is described by the following differential equation:

\[\dddot{x}=-\ddot{x}+9\dot{x}-x^2\dot{x}-5x\]

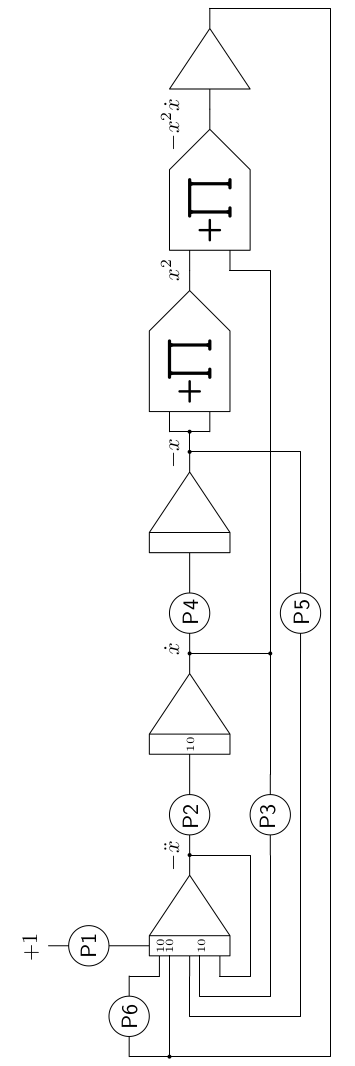
Scaling chaotic systems for implementation on an analog computer is typically a bit nasty which holds true for this particular case, too. A few numerical calculations using a simple Euler integration routine show that the term \(x^2\dot{x}\) has a domain exceeding \([-10^3:10^3]\) etc. Scaling is done by scaling down all inputs of one integrator by the same scale factor \(\lambda_i\) until no overload occurs anymore. Its output signal is then scaled back by \(\frac{1}{\lambda_i}\) before being fed to the next integrator, which is then scaled as well etc. Table 1 shows the values for the six coefficient potentiometers required in the computer setup shown in figure 1. The left column shows the parameters obtained by scaling “by the book” while the right column shows a parameter set that was obtained by tweaking some of the parameters manually. It is remarkable that the behaviour of the analog simulation shown in figure 2 is much more tame over a rather wide range of parameters than the numerical results shown in [Sprott 2010, p. 77]. Nevertheless, it is possible to find regions that exhibit chaotic behavior by some manual parameter variation.

Table1: Potentiometer settings for the jerk system

Potentiometer	Calculated	Manually obtained
P1	0.1	0.1
P2	0.75	0.75
P3	0.12	0.17
P4	0.2	0.2
P5	0.333	0.1
P6	0.333	1

Figure 1: Setup for the jerk system	Figure 2: Typical behavior of the jerk system

Nosé-Hoover Oscillator

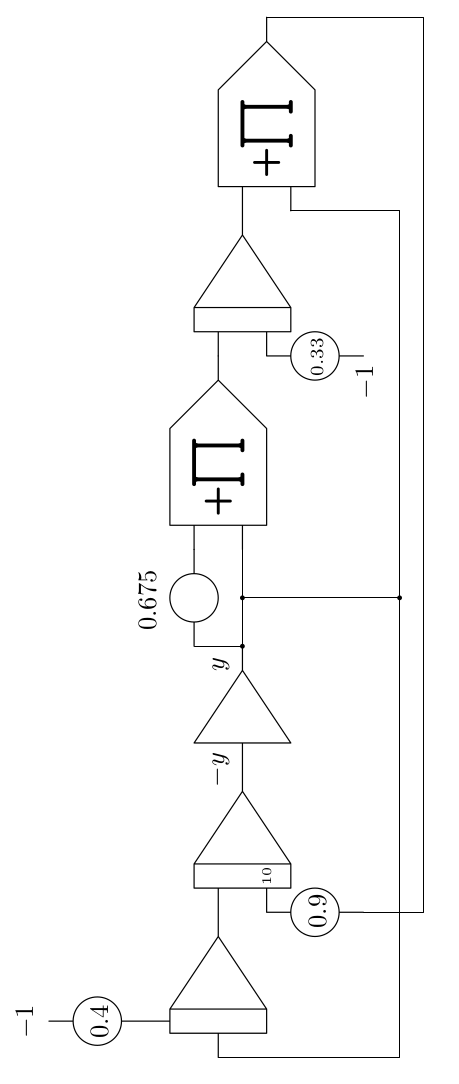
Another beutiful chaotic system is the Nosé-Hoover oscillator, an example of an autonomous conservative system which is described by the following set of coupled differential equations:

\[\begin{split}\begin{aligned} \dot{x}&=y\\ \dot{y}&=yz-x\\ \dot{z}&=1-y^2 \end{aligned}\end{split}\]

Scaling this system is quite mean, too, and yields the computer setup shown in figure 3, the results of which are shown in the mesmerizing oscilloscope screen capture shown in figure 4.

Figure 3: Setup for the Nosé-Hoover oscillator	Figure 4: Phase state plot of the Nosé-Hoover oscillator

References

[SPROTT 2011] Julien Clinton Sprott, Elegant Chaos – Algebraically Simple Chaotic Flows, World Scientific Publishing Co. Pte. Ltd, 2010