Rössler-attractor 1

An electronic analog computer is ideally suited to study continuous-time dynamical systems of which those showing chaotic behavior are not only quite interesting but also yield aesthetically pleasing phase space plots. The particular system treated below was developed and studied in 1976 by Otto Rössler. 2 This system is described by the following three coupled differential equations (DEQ)

\[\begin{split}\begin{aligned} \dot{x}&=-(y+z)\\ \dot{y}&=x+ay\\ \dot{z}&=b+z(x-c), \end{aligned}\end{split}\]

where \(a=1/5, b=1/5\), and \(c=5.7\). 3 A remarkable property of this particular system is that two of its three defining DEQs are linear.

Since variables in an analog computer are limited to the co-domain \([-1:+1]\) with \(-1\) and \(+1\) denoting the so-called machine units which are most often represented by \(\pm10\) V, 4 these equations must be scaled before setting up the computer. The main objective of scaling is to make sure that no variable exceeds \([-1:+1]\). In addition to that it is desirable that each variable takes on values of an as large subinterval of \([-1:+1]\) as possible in order to obtain the maximum precision from the analog computer.

The final set of scaled coupled DEQs for this problem looks like this:
\[\begin{split}\begin{aligned} \dot{x}&=-0.8y-2.3z\\ \dot{y}&=1.25x+a^*y\\ \dot{z}&=b^*+15z(x-c^*), \end{aligned}\end{split}\]

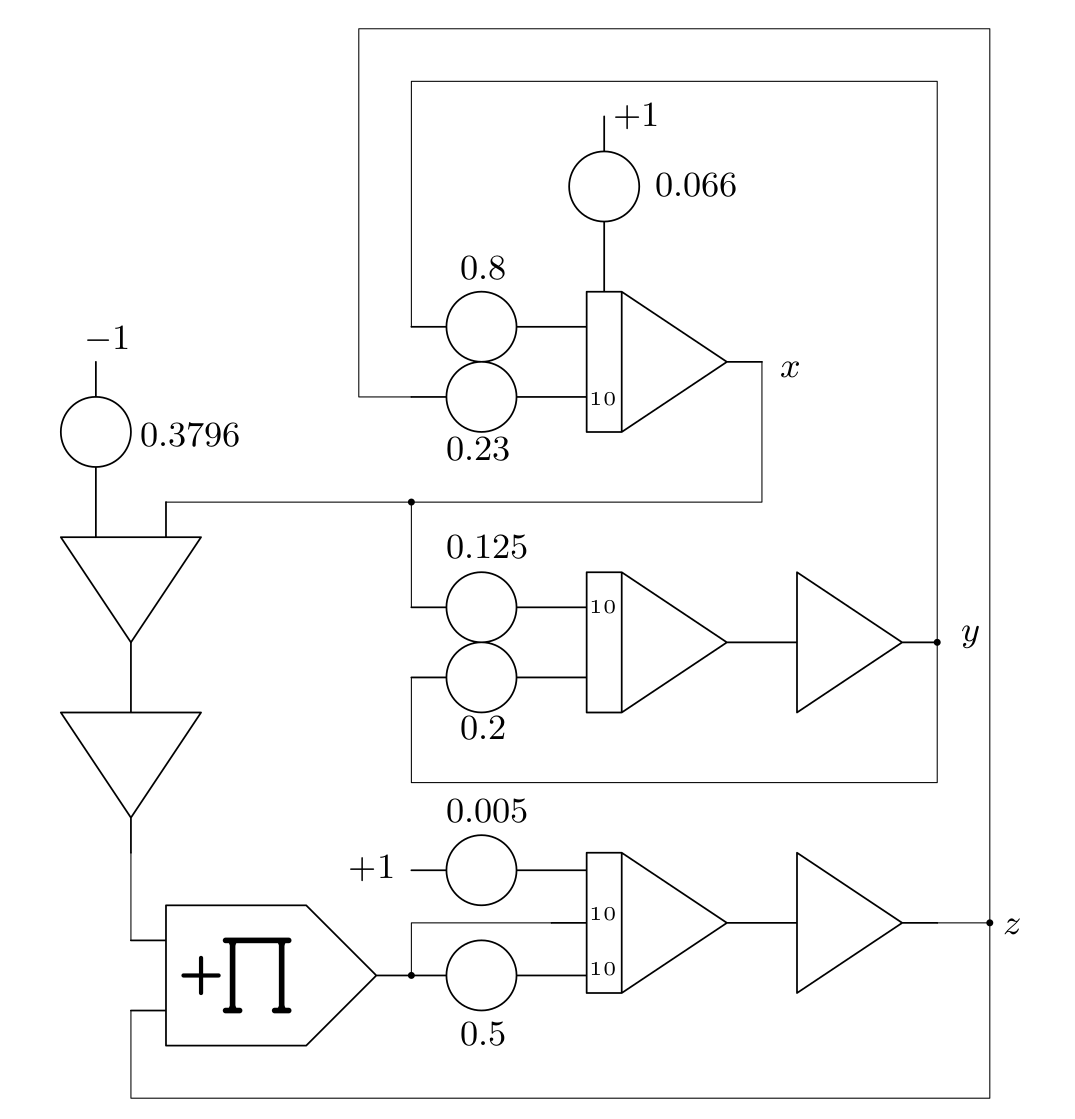
where \(a^*=0.2, b^*=0.005\), and \(c^*=0.3796\). The resulting computer setup is shown below:

image4

A typical analog computer setup for this circuit is shown below, the machine used is a minimal Model-1 from Analog Paradigm:

image1

The following photograph shows an \(x\)-\(y\)-plot of the attractor, photographed with ISO 100 and time constant \(k_0=10^3\) set on all three integrators involved:

image2

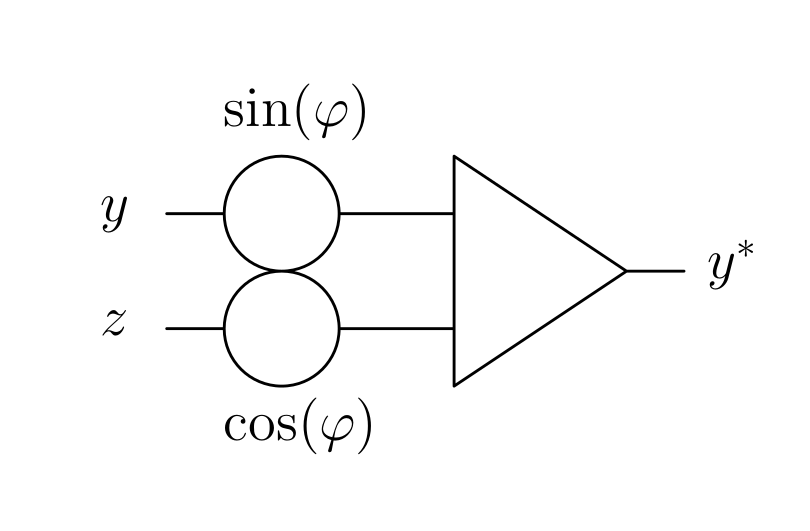
A beautiful picture can be obtained with a simple (static) 3d-projection of the attractor. Here \(x\) feeds one input of the oscillosope which is set to \(xy\)-mode, while the other input is fed from a summer yielding

\[y^*=-(y\sin(\varphi)+z\cos(\varphi)),\]

where the sine/cosine terms are directly set by coefficient potentiometers:

image5

Using these two coefficient potentiometers the angle of view is adjustable at will – one particular setting resulted in the following picture:

image3

1

I would like to thank professor Michael Brisk for spotting and correcting some errors in this article.

2

20th May 1940

3

\(\dot{x}\) denotes the first derivative of \(x\) with respect to time: \(\frac{\mathrm{d}x}{\mathrm{d}t}\) etc.

4

Vacuum tube based analog computers normally offered a voltage range of \(\pm100\) V.