Contents
Nonlinear chaos¶
An interesting chaotic system based on an absolute value function as the central nonlinear element has been described in . It is described by
This chaotic system is quite remarkable as it only has one parameter, \(\lambda\), controlling its behaviour.
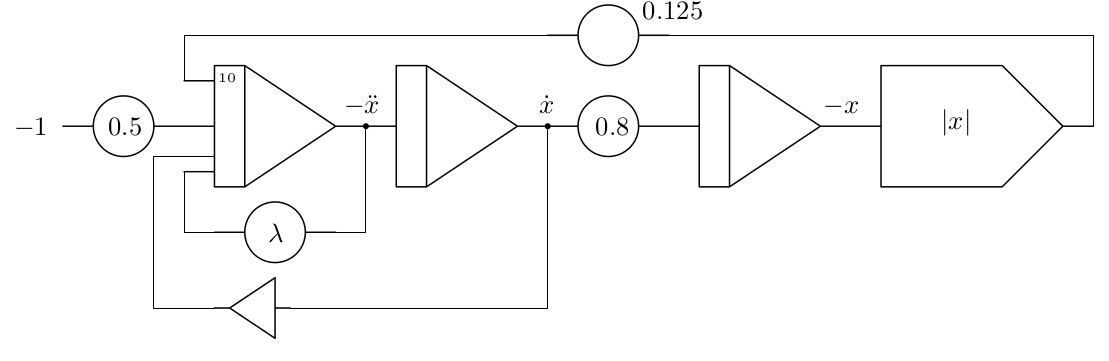
As written above values can get as big as about \(2.5\), so the equation has to be scaled in order to be implemented on an analog computer. Figure [pic_abs_chaos_program] shows the scaled program. The time constants of the integrators are set to \(k_0=10^3\).
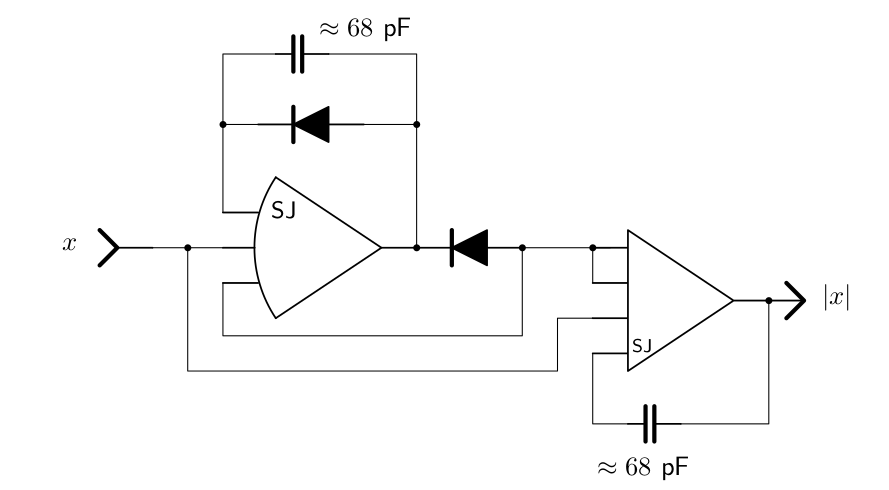
If no absolute value function is readily available on the analog computer being used, it can be setup as shown in figure [pic_abs_function]. The two capacitors shown stabilize the two summers and can be left out if there are no wild oscillations without them. Their value is quite uncritical and should be of the order of some \(10\) pF.
Figure [pic_abs_chaos_setup] shows the completed setup on an Analog Paradigm Model-1 analog computer. An example of a phase-space plot of this chaotic system with \(\lambda\approx0.62\) is shown in figure [pic_abs_chaos]. Here, \(-\ddot{x}\) and \(\dot{x}\) have been fed to the \(x\)- and \(y\)-inputs of the oscilloscope.
Nonlinear chaos circuit patched on an Analog Paradigm Model-1 analog computer
Phase-space plot of the chaotic attractor
9 Ken Kiers, Tim Klein, Jeff Kolb, Steve Price, “Chaos in a nonlinear analog computer”, in International Journal of Bifurcation and Chaos, Vol. 14, No. 8 (2004), pp. 2867–2873